La data science au service de la durabilité

Publié le 3 juin 2022 – Mis à jour le 9 novembre 2022
Date(s)

le 3 juin 2022

Zoom sur la recherche. Partitionnement de graphes et application à l’étude des relations entre les 17 Sustainable Development Goals.

La data science au service de la durabilité

Partitionnement de graphes et application à l’étude des relations entre les 17 Sustainable Development Goals.

En science des données, le partitionnement de graphes permet de structurer et de synthétiser l’information des relations entre sommets en découvrant des groupes disjoints au sein desquels les sommets sont fortement interconnectés. C’est un problème combinatoire qui fait l’objet de nombreux articles et trouve des applications dans de multiples disciplines. Nous décrivons ici notre contribution sur ce thème et nous appliquons celle-ci à l’étude des interdépendances entre les 17 Sustainable Development Goals. Ceci nous permet de souligner différents types d’axes, « composites » ou « unitaires », dans l’étude du développement durable des pays.

Le partitionnement de graphe : un problème difficile

Un graphe non-orienté valué est un ensemble de sommets connectés par un ensemble d’arêtes chacune doté d’un poids non négatif interprété ici comme une mesure d’affinité (ou de similarité). Il est représenté par une matrice d’adjacence carrée symétrique contenant des valeurs positives ou nulles. Le partitionnement d’un tel graphe consiste à segmenter les sommets en des groupes disjoints, aussi appelés clusters, au sein desquels les sommets sont mutuellement fortement connectés.

Le partitionnement permet de structurer l’information fouillis d’un graphe par le biais de quelques groupes singuliers et contribue ainsi à la découverte de connaissances. Cette tâche de classification automatique trouve des applications dans de nombreuses disciplines comme par exemple la détection de communautés dans des réseaux sociaux.

Toutefois, ce problème est combinatoire et en pratique, on utilise des heuristiques pour rechercher une solution approchée de la partition optimale. La méthode du spectral clustering qui peut être vue comme une adaptation des k-means aux graphes est une approche populaire.

Un nouveau modèle pour le partitionnement de graphe

Plusieurs travaux ont montré qu’il était pertinent, en amont du spectral clustering, de transformer le graphe d’affinités initial en un graphe d’affinités vérifiant plusieurs conditions sous-jacentes à un graphe représentant une véritable partition. Dans ce contexte, nous proposons un nouveau modèle et une procédure d’apprentissage qui transforment la matrice d’adjacence du graphe initial de sorte à ce qu’elle soit bistochastique et quasi-idempotente. L’originalité de la méthode, dénotée DSNI (Doubly Stochastic and Nearly-Idempotent), est la prise en compte de l’idempotence, contrainte difficile à traiter et qui a été négligée dans les travaux antérieurs. DSNI intègre astucieusement cette condition comme un terme de pénalité et conduit à un modèle d’optimisation qu’il est possible de résoudre efficacement avec des méthodes numériques avancées. De nombreuses expériences comparant DSNI à plusieurs techniques de la littérature montrent l’intérêt de l’approche.

La data science au service de la durabilité

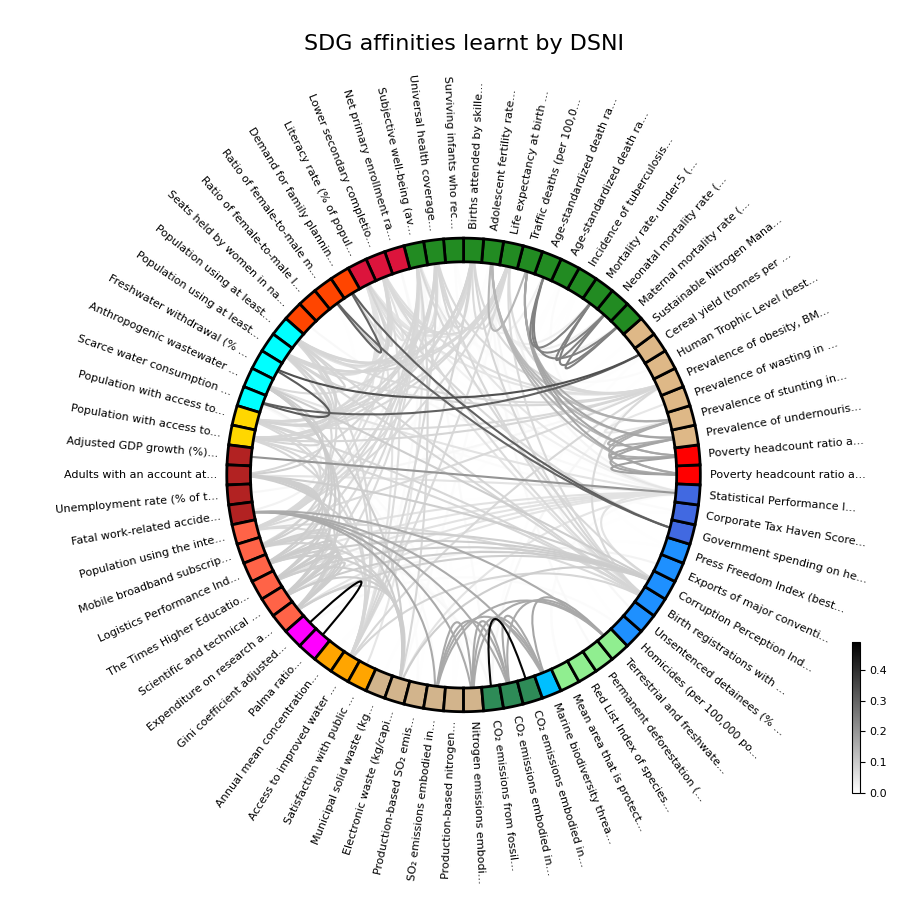
Le partitionnement de graphes trouve des applications en science de la durabilité. Pour illustrer ce propos, nous utilisons DSNI pour l’étude des relations entre les 17 Sustainable Development Goals (SDG) à partir des données du rapport 2021 de la SDSN (Sustainable Development Solutions Network) [1]. Cela concerne 74 indicateurs appartenant chacun à un des 17 SDG. Les observations de 163 pays ont été retenues. Nous examinons le graphe dont les sommets sont les 74 indicateurs et les affinités, les mesures de corrélation linéaire positives. Ce graphe, dense (1580 arêtes), est donné en entrée de DSNI qui procure en sortie un graphe parcimonieux (494 arêtes) bistochastique et quasi-idempotent. Le graphique en Figure 1 illustre les affinités obtenues par DSNI.
Figure 1
Ensuite, nous appliquons le spectral clustering sur ce graphe afin d’obtenir une véritable partition. Le nombre de clusters est fixé à 17 comme le nombre de SDG. Le but est de voir si, à nombre de groupes égale, les 74 indicateurs organisés selon les SDG se retrouvent dans les mêmes clusters ou pas. Les SDG et la partition des indicateurs obtenue sont exposés en Figure 2. A gauche sont représentés les 17 SDG, leur dénomination et leur couleur usuelles tandis qu’à droite sont exposés les clusters qui sont en gris. La taille d’un rectangle est proportionnelle au nombre d’indicateurs constituant soit un SDG soit un cluster. L’analyse montre d’une part, des groupes d’indicateurs inter-SDG et d’autre part, des indicateurs seuls. Par exemple, les clusters 13 et 2 regroupent de nombreux indicateurs provenant de multiples SDG. Ils peuvent être vus comme deux axes composites associés à deux aspects complémentaires du développement durable. A titre illustratif, le cluster 2 intègre la quasi-totalité des indicateurs Industry, Innovation and Infrastructure. Il se focalise ainsi sur cette thématique mais tout en intégrant des indicateurs d’autres SDG qui lui sont associés. A contrario, les clusters 14 et 15 par exemple, sont des singletons et mesurent ainsi des aspects très spécifiques du développement durable.
 

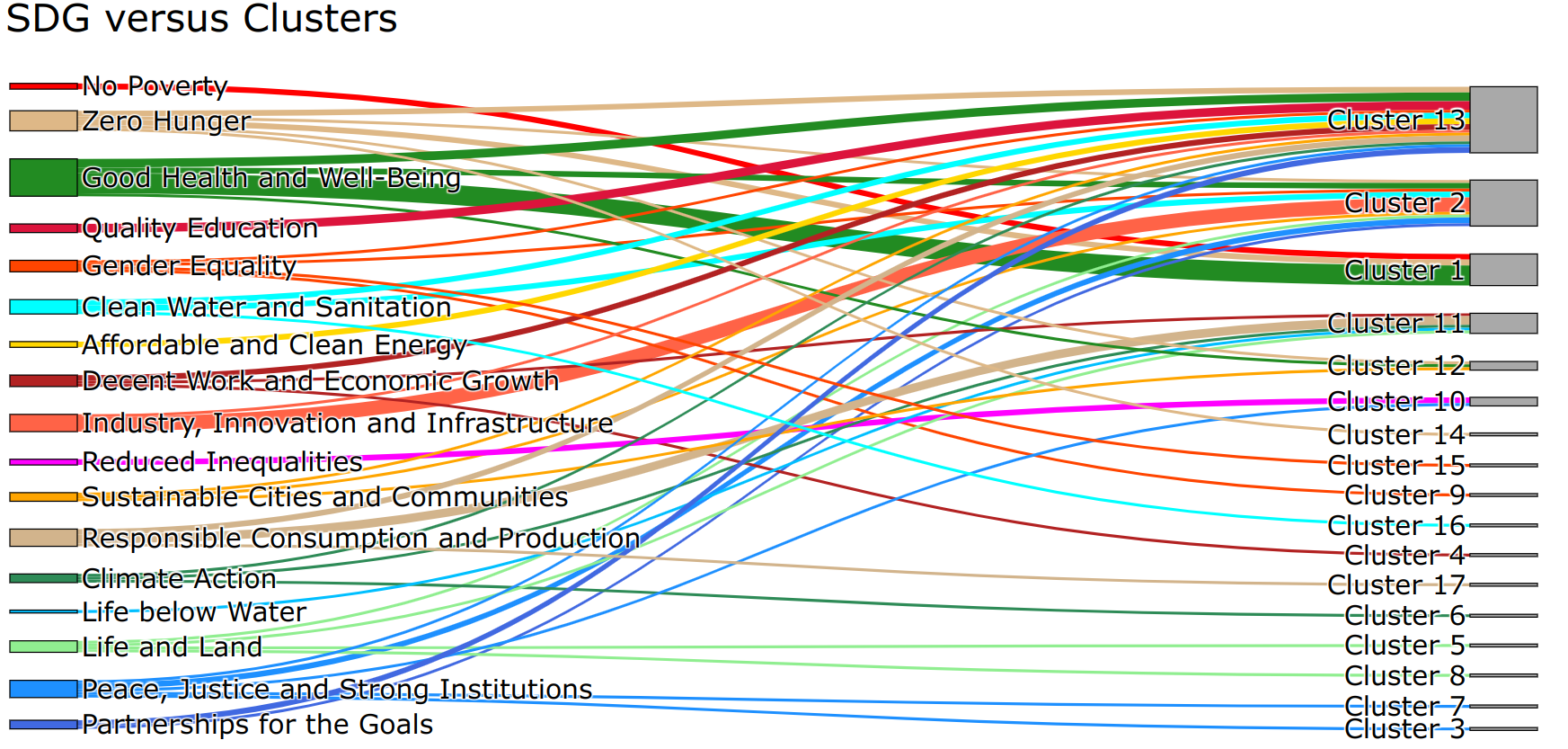Figure 2
A l’instar de cette application, le partitionnement de graphes peut apporter des contributions intéressantes pour l’analyse de données issues de l’économie du développement et de la science de la durabilité.

[1] Sachs, J., Kroll, C., Lafortune, G., Fuller, G., Woelm, F. (2021). The Decade of Action for the Sustainable Development Goals: Sustainable Development Report 2021.